diff --git a/README.md b/README.md index 8be7ec15e5fc46492c538ab918c72c6636adf042..1fb033841ebd0c4cadd3dcfe57425f5cc2ecfc03 100644 --- a/README.md +++ b/README.md @@ -1,11 +1,8 @@ # Course_MLPR -#### 介绍 -武汉大学机器学习与模式识别课程实验代码 +武汉大学机器学习与模式识别课程实验 -#### 使用说明 - -1. 大作业要求详见[`大作业`]() -2. 课后作业答案详见[`课后作业`]() -3. 实验指导及实验报告模板详见[`实验及报告`]() +1. 大作业要求详见[`大作业`](https://gitee.com/whu_mmap_cliang/Course_MLPR/tree/temp/%E5%A4%A7%E4%BD%9C%E4%B8%9A) +2. 课后作业答案详见[`课后作业`](https://gitee.com/whu_mmap_cliang/Course_MLPR/tree/temp/%E8%AF%BE%E5%90%8E%E4%BD%9C%E4%B8%9A) +3. 实验指导及实验报告模板详见[`实验及报告`](https://gitee.com/whu_mmap_cliang/Course_MLPR/tree/temp/%E5%AE%9E%E9%AA%8C%E5%8F%8A%E6%8A%A5%E5%91%8A) diff --git "a/\345\244\247\344\275\234\344\270\232/\346\225\260\346\215\256\351\233\206\344\275\277\347\224\250\350\257\264\346\230\216.md" "b/\345\244\247\344\275\234\344\270\232/\346\225\260\346\215\256\351\233\206\344\275\277\347\224\250\350\257\264\346\230\216.md" index dcfd75c4c43c77c3231bb3b0024d2b67fe48effc..bc92f4738b073fe722a7b9358dfd5713d4156991 100644 --- "a/\345\244\247\344\275\234\344\270\232/\346\225\260\346\215\256\351\233\206\344\275\277\347\224\250\350\257\264\346\230\216.md" +++ "b/\345\244\247\344\275\234\344\270\232/\346\225\260\346\215\256\351\233\206\344\275\277\347\224\250\350\257\264\346\230\216.md" @@ -86,9 +86,9 @@ ## 6 提交格式 -`小组名称.mat` +`姓名-学号.mat` - + 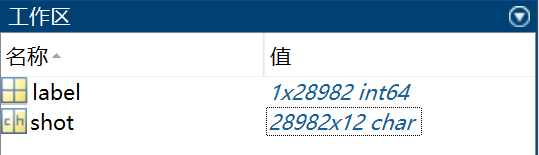e.g. label = 1, shot = 'shot222_33 ' diff --git "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/2-4-1.png" "b/\350\257\276\345\220\216\344\275\234\344\270\232/pics/2-4-1.png" deleted file mode 100644 index 132363d55d3b730ae31b866f3e27df5939ea6105..0000000000000000000000000000000000000000 Binary files "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/2-4-1.png" and /dev/null differ diff --git "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/2-4-2.png" "b/\350\257\276\345\220\216\344\275\234\344\270\232/pics/2-4-2.png" deleted file mode 100644 index e8e8a245a383d4fb80b5c677b9bf5bd5dfdeac29..0000000000000000000000000000000000000000 Binary files "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/2-4-2.png" and /dev/null differ diff --git "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/2-4-3.png" "b/\350\257\276\345\220\216\344\275\234\344\270\232/pics/2-4-3.png" deleted file mode 100644 index 979408f36cae87f3f7c965df94c48ba726bf497e..0000000000000000000000000000000000000000 Binary files "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/2-4-3.png" and /dev/null differ diff --git "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/56-3-1.png" "b/\350\257\276\345\220\216\344\275\234\344\270\232/pics/56-3-1.png" deleted file mode 100644 index d358df61061e2ca567f2ebcb5509ff713685173b..0000000000000000000000000000000000000000 Binary files "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/56-3-1.png" and /dev/null differ diff --git "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/78-4-1.png" "b/\350\257\276\345\220\216\344\275\234\344\270\232/pics/78-4-1.png" deleted file mode 100644 index aa50a942302999c6a7c37772e53f19a87b0fe6c2..0000000000000000000000000000000000000000 Binary files "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/78-4-1.png" and /dev/null differ diff --git "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/78-4-2.png" "b/\350\257\276\345\220\216\344\275\234\344\270\232/pics/78-4-2.png" deleted file mode 100644 index 364d4fec1ff69fbc3ffa33c5c953c85809691433..0000000000000000000000000000000000000000 Binary files "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/78-4-2.png" and /dev/null differ diff --git "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/78-4-3.png" "b/\350\257\276\345\220\216\344\275\234\344\270\232/pics/78-4-3.png" deleted file mode 100644 index 024adf688ca984497009a63836b2491f6fb442cc..0000000000000000000000000000000000000000 Binary files "a/\350\257\276\345\220\216\344\275\234\344\270\232/pics/78-4-3.png" and /dev/null differ diff --git "a/\350\257\276\345\220\216\344\275\234\344\270\232/\347\254\254\344\270\200\346\254\241\350\257\276\345\220\216\344\275\234\344\270\232.md" "b/\350\257\276\345\220\216\344\275\234\344\270\232/\347\254\254\344\270\200\346\254\241\350\257\276\345\220\216\344\275\234\344\270\232.md" index e65dc7273664b02d4a077d038cb110d1928e4c47..e88e2362f69a21178f591757c97ade68bf45962a 100644 --- "a/\350\257\276\345\220\216\344\275\234\344\270\232/\347\254\254\344\270\200\346\254\241\350\257\276\345\220\216\344\275\234\344\270\232.md" +++ "b/\350\257\276\345\220\216\344\275\234\344\270\232/\347\254\254\344\270\200\346\254\241\350\257\276\345\220\216\344\275\234\344\270\232.md" @@ -1,196 +1,210 @@ # 第一次课后作业解答 - +
## 第1讲 绪论 -1. **（1）对一位去医院做疾病诊断的病人而言，诊断技术的查全率重要还是查准率更重要？给出理由。** +
- **（2）对不断向你推荐商品的网站，该网站的商品推荐系统的查全率还是查准率你更关注？给出理由。** +1. （1）对一位去医院做疾病诊断的病人而言，诊断技术的查全率重要还是查准率更重要？给出理由。 - 做疾病诊断的病人肯定关注诊断技术的查全率。受网站推荐商品困扰的用户肯定关注推荐系统的查准率。 + （2）对不断向你推荐商品的网站，该网站的商品推荐系统的查全率还是查准率你更关注？给出理由。 - +> 做疾病诊断的病人肯定关注诊断技术的查全率。受网站推荐商品困扰的用户肯定关注推荐系统的查准率。 + +
-2. **（1） 简述数据模型的泛化能力与过拟合现象这两个概念；说明两者之间存在的一般性关系。** +2. （1） 简述数据模型的泛化能力与过拟合现象这两个概念；说明两者之间存在的一般性关系。 - **（2）借助模型的过拟合和泛化能力背后的原理，分析个人的专业学习与职业发展前景之间的关系（可以结合自己的经验）。** + （2）借助模型的过拟合和泛化能力背后的原理，分析个人的专业学习与职业发展前景之间的关系（可以结合自己的经验）。 - 模型的泛化能力就是指模型对新数据（模拟训练时未见到过的数据）时的预测与分类能力，即使这些新数据的分布与训练数据是相同的。模型的过拟合现象是指：模型对训练数据集的完美拟合（形象说，不仅拟合的规律性模式，也拟合了随机性噪声），导致模型的泛化能力下降。简单说，过拟合现象反映了模型专注于对细节的几乎是记忆性的模拟，而忽视了数据中一般性模式的发现。 +> 模型的泛化能力就是指模型对新数据（模拟训练时未见到过的数据）时的预测与分类能力，即使这些新数据的分布与训练数据是相同的。模型的过拟合现象是指：模型对训练数据集的完美拟合（形象说，不仅拟合的规律性模式，也拟合了随机性噪声），导致模型的泛化能力下降。简单说，过拟合现象反映了模型专注于对细节的几乎是记忆性的模拟，而忽视了数据中一般性模式的发现。 - +
## 第2讲 线性判别分类 -1. **线性回归与逻辑回归在模型设定、目标函数和求解算法上，有何相似和不同之处？** +
- 两种都是关于广义线性模型。线性回归模型的响应变量是连续定量数据，一般设定为服从正态分布（实际上就是认为观察噪声的分布为正态分布），主要用于数值预测。逻辑回归的响应变量则是离散的定性数据，其概率分布设定为二项分布（二分类）或多项分布（多分类问题）。 +1. 线性回归与逻辑回归在模型设定、目标函数和求解算法上，有何相似和不同之处？ -​ 两种方法的目标函数都使用数据集的似然函数，优化原则就是最大似然法。 +> 两种都是关于广义线性模型。线性回归模型的响应变量是连续定量数据，一般设定为服从正态分布（实际上就是认为观察噪声的分布为正态分布），主要用于数值预测。逻辑回归的响应变量则是离散的定性数据，其概率分布设定为二项分布（二分类）或多项分布（多分类问题）。两种方法的目标函数都使用数据集的似然函数，优化原则就是最大似然法。两种方法的参数求解，都是用梯度法、拟牛顿法（对二阶Hesse矩阵进行近似）进行求解。 -​ 两种方法的参数求解，都是用梯度法、拟牛顿法（对二阶Hesse矩阵进行近似）进行求解。 +
- +2. 如果你想将图片分类为户外／室内以及白天／黑夜。你应该实现两个逻辑回归分类器还是一个Softmax 回归分类器？ -2. **如果你想将图片分类为户外／室内以及白天／黑夜。你应该实现两个逻辑回归分类器还是一个Softmax 回归分类器？** +> 要将图片分类为户外／室内和白天／夜间，你应该训练两个逻辑回归分类器，因为这些类别之间并不是排他的（存在四种组合）。 - 要将图片分类为户外／室内和白天／夜间，你应该训练两个逻辑回归分类器，因为这些类别之间并不是排他的（存在四种组合）。 +
- +3. （1）逻辑回归实际上是用样本点的回归函数值的logistic变换值来拟合样本点属于正类的概率。简要说明这种建模方法的合理性和不合理之处。 -3. **（1）逻辑回归实际上是用样本点的回归函数值的logistic变换值来拟合样本点属于正类的概率。简要说明这种建模方法的合理性和不合理之处。** + （2）能否用正态随机变量的累积分布函数来替换logistic函数，作为逻辑回归中的概率变换函数？为什么？还能想到其他的可用于逻辑回归的变换函数吗？ - **（2）能否用正态随机变量的累积分布函数来替换logistic函数，作为逻辑回归中的概率变换函数？为什么？还能想到其他的可用于逻辑回归的变换函数吗？** +> （1）合理之处：在某些情况下，数据点离类间边界的距离，的确可以反映该数据点属于某类的“程度”，把程度理解为“类的隶属度”也是可以的，尤其在分类应用中，主要目标就是离类间边界越远越好。但是不合理之处在于，逻辑回归分类本质上是一种概率分类：先获得类别的概率分布，再利用数据点的在模型下计算出的“概率值”进行分类，而概率分类存在一个共同的问题，就是对明显的线性可分数据，也能产生错误的判别。

+（2）可以用正态分布的累积分布函数$\phi(x)$，可以代替逻辑回归logistic函数，其反函数就是Φ-1(p)即使下p分位点，反函数类似于logit变换，也是可以把一个[0, 1之间的正数变换到整个实数轴，且是严格单调增的。其实这就是所谓probit回归。但是这里有一个问题，这个函数的导数不方便计算，因此现在不再使用（其实逻辑回归就是从早期的probit回归演变而来的）。 - 合理之处：在某些情况下，数据点离类间边界的距离，的确可以反映该数据点属于某类的“程度”，把程度理解为“类的隶属度”也是可以的，尤其在分类应用中，主要目标就是离类间边界越远越好。但是不合理之处在于，逻辑回归分类本质上是一种概率分类：先获得类别的概率分布，再利用数据点的在模型下计算出的“概率值”进行分类，而概率分类存在一个共同的问题，就是对明显的线性可分数据，也能产生错误的判别。 - - 可以用正态分布的累积分布函数Φ(x)，可以代替逻辑回归logistic函数，其反函数就是Φ-1(p)即使下p分位点，反函数类似于logit变换，也是可以把一个[0, 1之间的正数变换到整个实数轴，且是严格单调增的。其实这就是所谓probit回归。但是这里有一个问题，这个函数的导数不方便计算，因此现在不再使用（其实逻辑回归就是从早期的probit回归演变而来的）。 +
- +4. 一个三类问题，其判别函数为$d_1(\boldsymbol{X}) = x_1+2x_2-4$，$d_2(\boldsymbol{X}) = x_1-4x_2+4$，$d_3(\boldsymbol{X})=-x_1+3$。 -4. **一个三类问题，其判别函数为$d_1(\boldsymbol{X}) = x_1+2x_2-4$，$d_2(\boldsymbol{X}) = x_1-4x_2+4$，$d_3(\boldsymbol{X})=-x_1+3$** + （1）设这些函数是在多类情况1条件下确定的，绘出判别界面及每一模式类别的区域。 - **（1） 设这些函数是在多类情况1条件下确定的，绘出判别界面及每一模式类别的区域。** + （2）设为多类情况2，并使$d_{12}(\boldsymbol{X})=d_1(\boldsymbol{X})$，$d_{13}(\boldsymbol{X})=d_2(\boldsymbol{X})$，$d_{23}(\boldsymbol{X})=d_3(\boldsymbol{X})$，绘出判别界面及每一模式类别的区域。 - **（2） 设为多类情况2，并使$d_{12}(\boldsymbol{X})=d_1(\boldsymbol{X})$，$d_{13}(\boldsymbol{X})=d_2(\boldsymbol{X})$，$d_{23}(\boldsymbol{X})=d_3(\boldsymbol{X})$，绘出判别界面及每一模式类别的区域。** + （3） 设$d_1(\boldsymbol{X})$，$d_2(\boldsymbol{X})$和$d_3(\boldsymbol{X})$是在多类情况3的条件下确定的，绘出其判别界面及每一模式类别的区域。 + +
+解答： + +（1）多类情况1时的判别界面及每一模式类别的区域如图1所示。 - **（3） 设$d_1(\boldsymbol{X})$，$d_2(\boldsymbol{X})$和$d_3(\boldsymbol{X})$是在多类情况3的条件下确定的，绘出其判别界面及每一模式类别的区域。** - - - - （1）多类情况1时的判别界面及每一模式类别的区域如下图所示。 - - 2-4-1 -​ （2）多类情况2时的判别界面及每一模式类别的区域如下图所示。 +（2）多类情况2时的判别界面及每一模式类别的区域如图2所示。 -2-4-2 -​ （3）多类情况3时三个判别界面方程为： +（3）多类情况3时三个判别界面方程为： -​ $d_1(\boldsymbol{X})-d_2(\boldsymbol{X})=(x_1+2x_2-4)-(x_1-4x_2+4)=6x_2-8=0$，即$3x_2-4=0$ +$d_{1}(\boldsymbol{X})-d_{2}(\boldsymbol{X})=(x_{1}+2x_{2}-4)-(x_{1}-4x_{2}+4)=6x_{2}-8=0$，即$3x_{2}-4=0$ -​ $d_1(\boldsymbol{X})-d_3(\boldsymbol{X})=(x_1+2x_2-4)-(-x_1+3)=2x_1+2x_2-7=0$ +$d_1(\boldsymbol{X})-d_3(\boldsymbol{X})=(x_1+2x_2-4)-(-x_1+3)=2x_1+2x_2-7=0$ -​ $d_2(\boldsymbol{X})-d_3(\boldsymbol{X})=(x_1-4x_2+4)-(-x_1+3)=2x_1-4x_2+1=0$ +$d_2(\boldsymbol{X})-d_3(\boldsymbol{X})=(x_1-4x_2+4)-(-x_1+3)=2x_1-4x_2+1=0$ -​ 满足$d_1(\boldsymbol{X})-d_2(\boldsymbol{X})>0$且$d_1(\boldsymbol{X})-d_3(\boldsymbol{X})>0$的区域属于$\omega_1$类分布区域。 +满足$d_1(\boldsymbol{X})-d_2(\boldsymbol{X})>0$且$d_1(\boldsymbol{X})-d_3(\boldsymbol{X})>0$的区域属于$\omega_1$类分布区域。 -​ 满足$d_2(\boldsymbol{X})-d_1(\boldsymbol{X})>0$且$d_2(\boldsymbol{X})-d_3(\boldsymbol{X})>0$的区域属于$\omega_2$类分布区域。 +满足$d_2(\boldsymbol{X})-d_1(\boldsymbol{X})>0$且$d_2(\boldsymbol{X})-d_3(\boldsymbol{X})>0$的区域属于$\omega_2$类分布区域。 -​ 满足$d_3(\boldsymbol{X})-d_1(\boldsymbol{X})>0$且$d_3(\boldsymbol{X})-d_2(\boldsymbol{X})>0$的区域属于$\omega_3$类分布区域。 +满足$d_3(\boldsymbol{X})-d_1(\boldsymbol{X})>0$且$d_3(\boldsymbol{X})-d_2(\boldsymbol{X})>0$的区域属于$\omega_3$类分布区域。 -​ 判别界面及各模式类的区域如下图所示。 +判别界面及各模式类的区域如图3所示。 -2-4-3 +
+
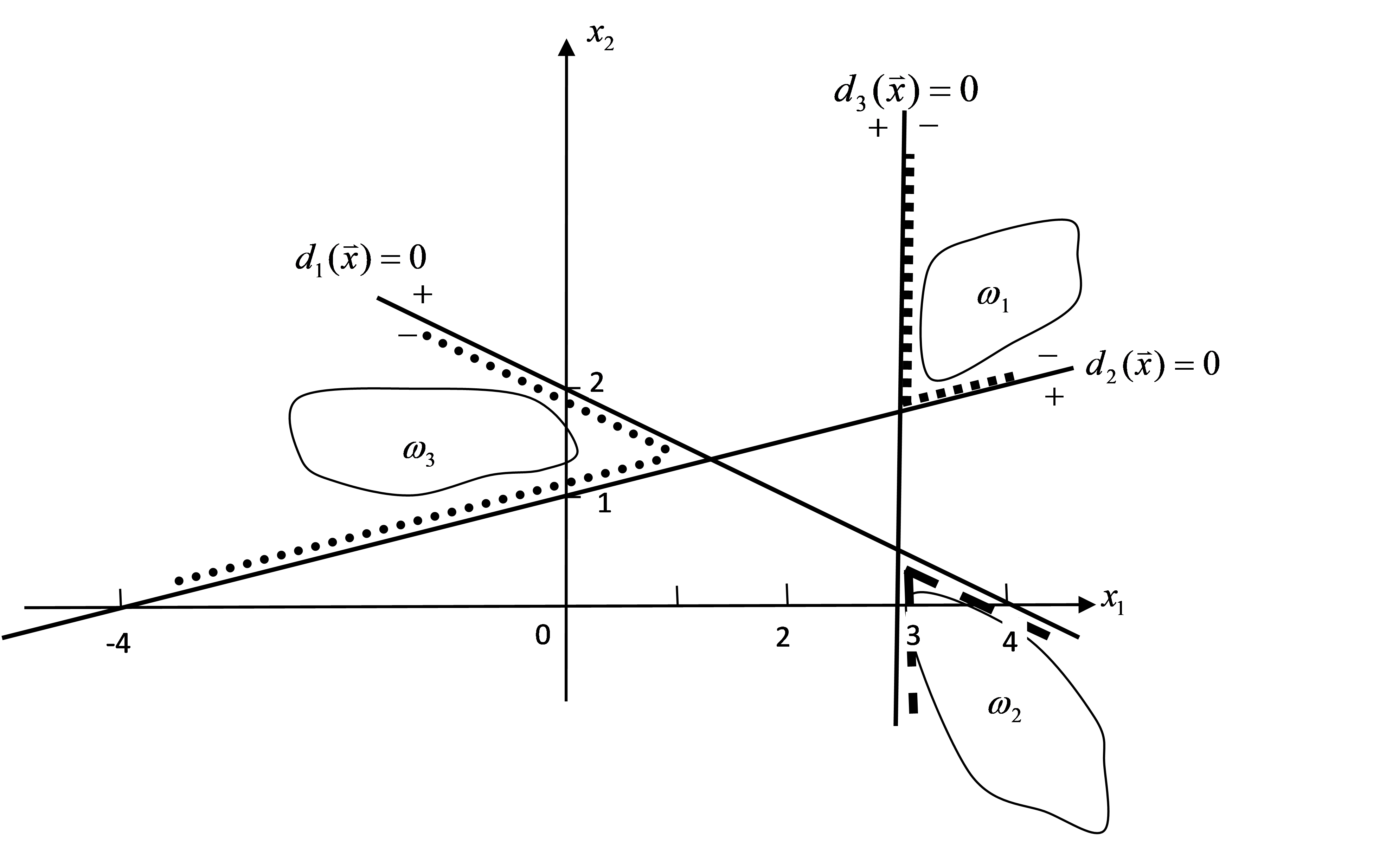
图1
+
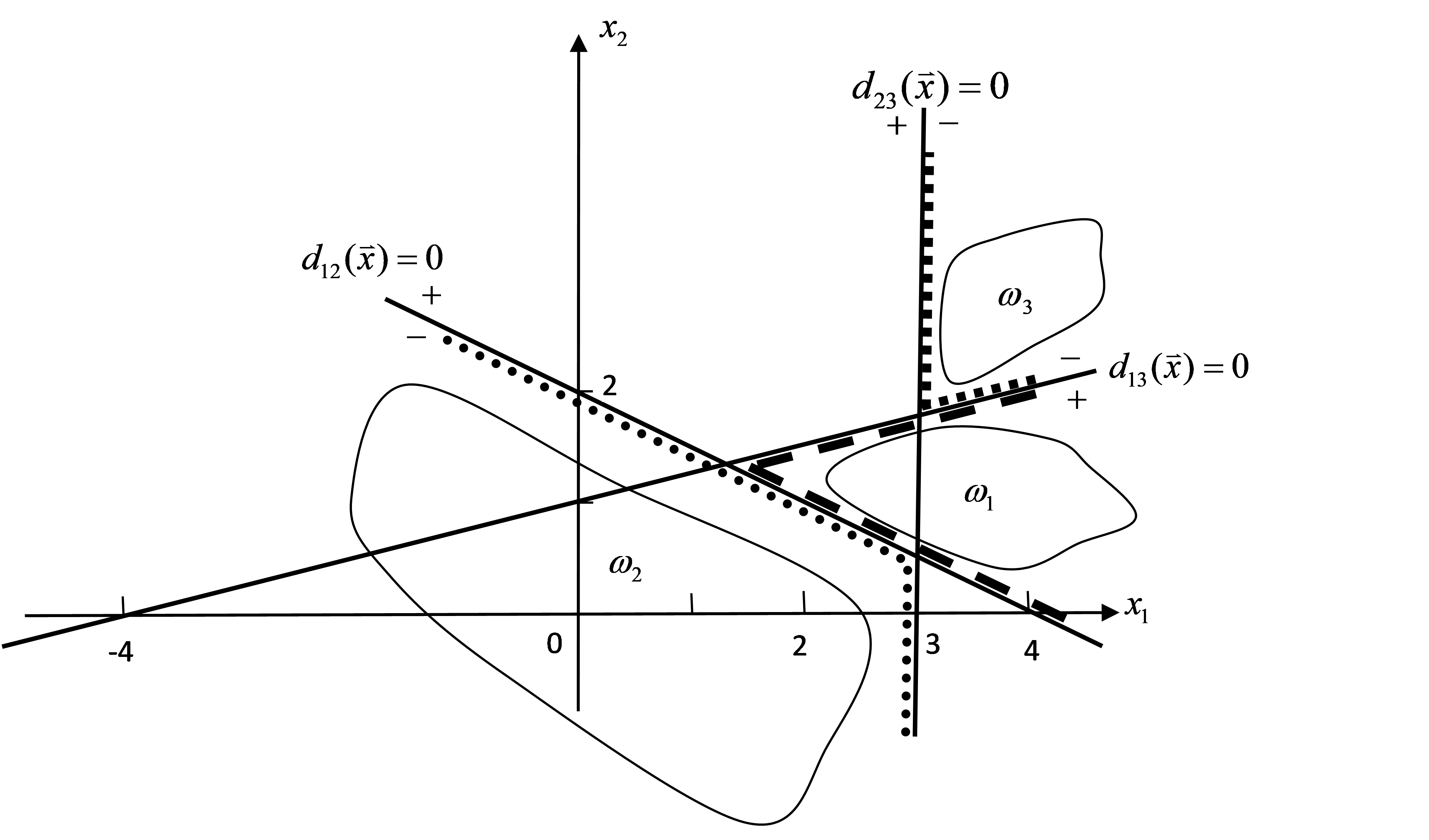
图2
+
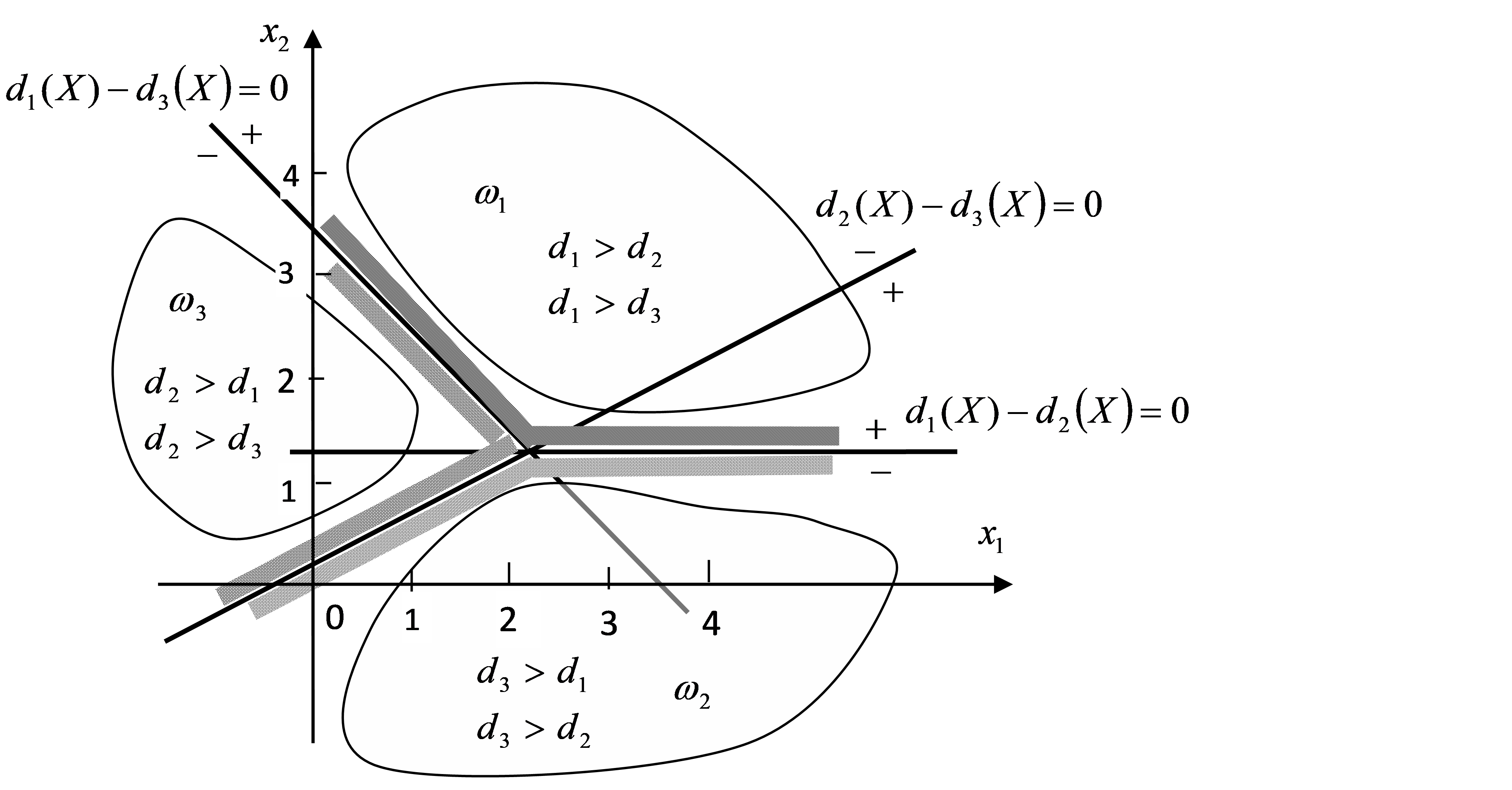
图3
+
+ ## 第3、4讲 概率分类 -1. **就分类而言，在模型训练前，对一个样本所来自的总体的类别变量分布的先验知识，与在模型训练后对该类别变量分布的后验知识，主要区别是什么？在什么意义下，两种是一致的？** +
- 关于参数（这里是样本所属总体的类别变量的分布参数）的先验知识是指在进行实验前获得的关于参数分布的信息，而关于参数的后验分布则是值在结合了样本中关于总体参数的信息后关于参数分布的信息。在这个意义上，先验信息和后验信息是一致的，都是关于参数的分布知识，区别就在于是否利用了某个样本或样本集。因此，谈先验、后验之分需要针对某个样本集来说。**昨天的后验就是今天的先验，今天的先验就是明天的后验！** +1. 就分类而言，在模型训练前，对一个样本所来自的总体的类别变量分布的先验知识，与在模型训练后对该类别变量分布的后验知识，主要区别是什么？在什么意义下，两种是一致的？ - +> 关于参数（这里是样本所属总体的类别变量的分布参数）的先验知识是指在进行实验前获得的关于参数分布的信息，而关于参数的后验分布则是值在结合了样本中关于总体参数的信息后关于参数分布的信息。在这个意义上，先验信息和后验信息是一致的，都是关于参数的分布知识，区别就在于是否利用了某个样本或样本集。因此，谈先验、后验之分需要针对某个样本集来说。**昨天的后验就是今天的先验，今天的先验就是明天的后验！** + +
+ +2. 朴素贝叶斯分类方法的基本假设是什么？试举一例说明该假设的合理性。 + +> 基本假设就是在已知样本的类别时，样本的各个特征（属性）之间是条件独立的。比如，设“一个人是否高收入”为样本的类别（Y=1表示高收入），同时设“一个人是否经常购买高档白酒”为属性X1（X1=1表示经常购买高档白酒），设“一个人是否经常购买高档服装”为属性X2（X2=1表示经常购买高档服装）。（1）在不知道一个人的收入情况下，也就是说在人群总体中进行一般调查时，从计算角度看，属性X1和属性X2肯定存在一定的“相关关系”（也就是说，肯定有部分人员既经常购买高档白酒，也经常购买高档服装），因此不能排除这两个属性在人群总体中存在一定的依赖关系。（2）但是在知道了一个人是高收入的情况下，“是否经常购买高档白酒”与“是否经常购买高档服装”就是互不依赖的，因为此时这两个属性都是真正的原因“高收入”引起的，而不是相互引起的（经常买高品质白酒的人，并一定会经常买高档衣服，反之亦然），因此这两个属性，在已知“一个人是高收入”的条件下，可以认为是条件独立的。 + +
+ +3. 假设在某个地区的疾病普查中，异常细胞（$\omega_1$）和正常细胞（$\omega_2$）的先验概率分别为$P(\omega_1)=0.1$，$P(\omega_2)=0.9$。现有一待识别细胞，其观察值为$X$，从类概率密度分布曲线上查得$p(X|\omega_1)=0.4$，$p(X|\omega_2)=0.2$。试对该细胞利用最小错误率贝叶斯决策规则进行分类。 -2. **朴素贝叶斯分类方法的基本假设是什么？试举一例说明该假设的合理性。 ** +
+解1： - 基本假设就是在已知样本的类别时，样本的各个特征（属性）之间是条件独立的。比如，设“一个人是否高收入”为样本的类别（Y=1表示高收入），同时设“一个人是否经常购买高档白酒”为属性X1（X1=1表示经常购买高档白酒），设“一个人是否经常购买高档服装”为属性X2（X2=1表示经常购买高档服装）。（1）在不知道一个人的收入情况下，也就是说在人群总体中进行一般调查时，从计算角度看，属性X1和属性X2肯定存在一定的“相关关系”（也就是说，肯定有部分人员既经常购买高档白酒，也经常购买高档服装），因此不能排除这两个属性在人群总体中存在一定的依赖关系。（2）但是在知道了一个人是高收入的情况下，“是否经常购买高档白酒”与“是否经常购买高档服装”就是互不依赖的，因为此时这两个属性都是真正的原因“高收入”引起的，而不是相互引起的（经常买高品质白酒的人，并一定会经常买高档衣服，反之亦然），因此这两个属性，在已知“一个人是高收入”的条件下，可以认为是条件独立的。 +$P\left(\omega_{2} \mid X\right)=\frac{p\left(X \mid \omega_{2}\right) P\left(\omega_{2}\right)}{\sum_{i=1}^{2} p\left(X \mid \omega_{i}\right) P\left(\omega_{i}\right)}=\frac{0.2\times 0.9}{0.2\times 0.9+0.4\times 0.1}\approx 0.818$ + +$P\left(\omega_{1} \mid X\right)=\frac{p\left(X \mid \omega_{1}\right) P\left(\omega_{1}\right)}{\sum_{i=1}^{2} p\left(X \mid \omega_{i}\right) P\left(\omega_{i}\right)}=\frac{0.4\times 0.1}{0.2\times 0.9+0.4\times 0.1}\approx 0.182$ + +$\because P\left(\omega_{2} \mid X\right)>P\left(\omega_{1} \mid X\right) \qquad \therefore X\in \omega_2$ +解2： -3. **假设在某个地区的疾病普查中，异常细胞（$\omega_1$）和正常细胞（$\omega_2$）的先验概率分别为$P(\omega_1)=0.1$，$P(\omega_2)=0.9$。现有一待识别细胞，其观察值为$X$，从类概率密度分布曲线上查得$p(X|\omega_1)=0.4$，$p(X|\omega_2)=0.2$。试对该细胞利用最小错误率贝叶斯决策规则进行分类。** +$p(X\mid \omega_2)P(\omega_2)=0.2\times 0.9=0.18,\quad p(X\mid \omega_1)P(\omega_1)=0.4\times 0.1=0.04$ - 解1： +$\because p(X\mid \omega_2)P(\omega_2)>p(X\mid \omega_1)P(\omega_1)\quad \therefore X\in \omega_2$ +
-$$ -P\left(\omega_{2} \mid X\right)=\frac{p\left(X \mid \omega_{2}\right) P\left(\omega_{2}\right)}{\sum_{i=1}^{2} p\left(X \mid \omega_{i}\right) P\left(\omega_{i}\right)}=\frac{0.2\times 0.9}{0.2\times 0.9+0.4\times 0.1}\approx 0.818\\ -P\left(\omega_{1} \mid X\right)=\frac{p\left(X \mid \omega_{1}\right) P\left(\omega_{1}\right)}{\sum_{i=1}^{2} p\left(X \mid \omega_{i}\right) P\left(\omega_{i}\right)}=\frac{0.4\times 0.1}{0.2\times 0.9+0.4\times 0.1}\approx 0.182\\ -\because P\left(\omega_{2} \mid X\right)>P\left(\omega_{1} \mid X\right) \qquad \therefore X\in \omega_2 -$$ +
-​ 解2： -$$ -p(X\mid \omega_2)P(\omega_2)=0.2\times 0.9=0.18,\quad p(X\mid \omega_1)P(\omega_1)=0.4\times 0.1=0.04\\ -\because p(X\mid \omega_2)P(\omega_2)>p(X\mid \omega_1)P(\omega_1)\quad \therefore X\in \omega_2 -$$ +4. 对前一题中两类细胞的分类问题（异常细胞$\omega_1$，正常细胞$\omega_2$），除已知的数据外，若损失函数的值分别为$L_{11}=0$，$L_{21}=6$，$L_{12}=1$，$L_{22}=0$，试用最小风险贝叶斯决策规则对细胞进行分类。 +
+解1：当$X$被判为$\omega_1$类时： -4. **对前一题中两类细胞的分类问题（异常细胞$\omega_1$，正常细胞$\omega_2$），除已知的数据外，若损失函数的值分别为$L_{11}=0$，$L_{21}=6$，$L_{12}=1$，$L_{22}=0$，试用最小风险贝叶斯决策规则对细胞进行分类。** +$d_1(X)=L_{11}p(X\mid \omega_1)P(\omega_1)+L_{12}p(X\mid \omega_2)P(\omega_2)=0\times 0.4\times 0.1+1\times 0.2 \times 0.9=0.18$ - 解1：当$X$被判为$\omega_1$类时： - $$ - d_1(X)=L_{11}P(X\mid \omega_1)P(\omega_1)+L_{12}p(X\mid \omega_2)P(\omega_2)=0\times 0.4\times 0.1+1\times 0.2 \times 0.9=0.18 - $$ - 当*X*被判为$\omega_2$类时： - $$ - d_2(X)=L_{21}p(X\mid \omega_1)P(\omega_1)+L_{22}p(X\mid \omega_2)P(\omega_2)=6\times 0.4\times 0.1+0\times 0.2 \times 0.9=0.24 - $$ - $\because d_1(X)\theta_{12}, \quad \therefore X\in \omega_1$ +$d_2(X)=L_{21}p(X\mid \omega_1)P(\omega_1)+L_{22}p(X\mid \omega_2)P(\omega_2)=6\times 0.4\times 0.1+0\times 0.2 \times 0.9=0.24$ - +$\because d_2(X)>d_1(X), \quad \therefore X\in \omega_1$ + +
+解2： + +$l_{12}(X)=\frac{p(X\mid \omega_1)}{p(X\mid \omega_2)}=\frac{0.4}{0.2}=2$ -5. **考虑下表中的数据集。** - -| **样本序号** | **A** | **B** | **C** | **类别** | -| ------------ | ----- | ----- | ----- | -------- | -| 1 | 0 | 0 | 1 | - | -| 2 | 1 | 0 | 1 | + | -| 3 | 0 | 1 | 0 | - | -| 4 | 1 | 0 | 0 | - | -| 5 | 1 | 0 | 1 | + | -| 6 | 0 | 0 | 1 | + | -| 7 | 1 | 1 | 0 | - | -| 8 | 0 | 0 | 0 | - | -| 9 | 0 | 1 | 0 | + | -| 10 | 1 | 1 | 1 | + | +$\theta_{12}=\frac{(L_{12}-L_{22})P(\omega_{2})}{(L_{21}-L_{11})P(\omega_{1})}=\frac{(1-0)\times 0.9}{(6-0)\times 0.1}=1.5$ +$\because l_{12}(X)>\theta_{12}, \quad \therefore X\in \omega_{1}$ +
+ +
+ +5. 考虑下表中的数据集。 + + | **样本序号** | **A** | **B** | **C** | **类别** | + | ------------ | ----- | ----- | ----- | -------- | + | 1 | 0 | 0 | 1 | - | + | 2 | 1 | 0 | 1 | + | + | 3 | 0 | 1 | 0 | - | + | 4 | 1 | 0 | 0 | - | + | 5 | 1 | 0 | 1 | + | + | 6 | 0 | 0 | 1 | + | + | 7 | 1 | 1 | 0 | - | + | 8 | 0 | 0 | 0 | - | + | 9 | 0 | 1 | 0 | + | + | 10 | 1 | 1 | 1 | + | + -​ **（1）估计以下条件概率$P(A=1|+)$，$P(B=1|+)$，$P(C=1|+)$，$P(A=1|-)$，$P(B=1|-)$，$P(C=1|-)$ 。** + （1）估计以下条件概率$P(A=1|+)$，$P(B=1|+)$，$P(C=1|+)$，$P(A=1|-)$，$P(B=1|-)$，$P(C=1|-)$ 。 + + （2）根据估计出的条件概率，使用朴素贝叶斯方法预测样本$(A=1,B=1,C=1)$的类别。 + + （3）比较$P(A=1)$，$P(B=1)$和$P(A=1,B=1)$，陈述变量$A$、$B$之间的统计关系。 -​ **（2）根据估计出的条件概率，使用朴素贝叶斯方法预测样本$(A=1,B=1,C=1)$的类别。** + （4）比较$P(A=1|+)$，$P(B=1|+)$和$P(A=1,B=1|+)$，给定类$＋$，变量$A$、$B$独立吗？ -​ **（3）比较$P(A=1)$，$P(B=1)$和$P(A=1,B=1)$，陈述变量$A$、$B$之间的统计关系。** +
+解答：（陈封能，第2版，第4章，习题8） -​ **（4）比较$P(A=1|+)$，$P(B=1|+)$和$P(A=1,B=1|+)$，给定类$＋$，变量$A$、$B$独立吗？** +（1）根据数据集计算的： -​ 解答：（陈封能，第2版，第4章，习题8） +$P(A=1|+)=0.6, P(B=1|+)=0.4, P(C=1|+)=0.8, P(A=1|-)=0.4,P(B=1|-)=0.4,P(C=1|-)=0.2$ -​ （1）根据数据集计算的： -$$ -P(A=1|+)=0.6, P(B=1|+)=0.4, P(C=1|+)=0.8\\P(A=1|-)=0.4,P(B=1|-)=0.4,P(C=1|-)=0.2 -$$ -​ （2）记$R:(A=1,B=1,C=1)$为测试样本。为计算$P(+|R)$、$P(-|R)$，根据贝叶斯公式，需计算$P(+)$、$P(-)$、$P(R|+)$、$P(R|-)$。根据数据集可以计算：$P(+)=P(-)=0.5$，而 -$$ -P(R|+)=P(A=1|+)\times P(B=1|+)\times P(C=1|+) = 0.192 \\ -P(R|-)=P(A=1|-)\times P(B=1|-)\times P(C=1|-) = 0.032 -$$ -​ 于是有$P(+|R)>P(-|R)$，因此该测试样本应该判为类$+$。 -​ （3） -$$ -P(A=1)=0.5，P(B=1)=0.4，P(A=1,B=1)=0.2，\\ +（2）记$R:(A=1,B=1,C=1)$为测试样本。为计算$P(+|R)$、$P(-|R)$，根据贝叶斯公式，需计算$P(+)$、$P(-)$、$P(R|+)$、$P(R|-)$。 -P(A=1,B=1)=P(A=1)\times P(B=1) -$$ -​ 因此，可认为$A$、$B$是互相独立的。 +根据数据集可以计算$P(+)=P(-)=0.5$，而 -​ （4）根据数据集计算得： -$$ -P(A=1|+)=0.6, P(B=1|+)=0.4, P(A=1,B=1|+)=0.2 -$$ -​ 此时： -$$ -P(A=1,B=1|+)\neq P(A=1|+)\times P(B=1|+) -$$ -​ 因此可以认为，在给定了类别$+$的条件下，变量$A$和变量$B$并不统计独立。 +$P(R|+)=P(A=1|+)\times P(B=1|+)\times P(C=1|+) = 0.192$ + +$P(R|-)=P(A=1|-)\times P(B=1|-)\times P(C=1|-) = 0.032$ + +于是有$P(+|R)>P(-|R)$，因此该测试样本应该判为类$+$。 + + +（3）$P(A=1)=0.5，P(B=1)=0.4，P(A=1,B=1)=0.2,$ + +$P(A=1,B=1)=P(A=1)\times P(B=1)$ + +因此，可认为$A$、$B$是互相独立的。 + + +（4）根据数据集计算得：$P(A=1|+)=0.6, P(B=1|+)=0.4, P(A=1,B=1|+)=0.2$ + +此时$P(A=1,B=1|+)\neq P(A=1|+)\times P(B=1|+)$ +因此可以认为，在给定了类别$+$的条件下，变量$A$和变量$B$并不统计独立。 +
diff --git "a/\350\257\276\345\220\216\344\275\234\344\270\232/\347\254\254\344\272\214\346\254\241\350\257\276\345\220\216\344\275\234\344\270\232.md" "b/\350\257\276\345\220\216\344\275\234\344\270\232/\347\254\254\344\272\214\346\254\241\350\257\276\345\220\216\344\275\234\344\270\232.md" index eb52f876bfee498bdd95e04f83eee0be82adbb71..5c86650399d887afba5e1d60ed87e9a2371b3ff2 100644 --- "a/\350\257\276\345\220\216\344\275\234\344\270\232/\347\254\254\344\272\214\346\254\241\350\257\276\345\220\216\344\275\234\344\270\232.md" +++ "b/\350\257\276\345\220\216\344\275\234\344\270\232/\347\254\254\344\272\214\346\254\241\350\257\276\345\220\216\344\275\234\344\270\232.md" @@ -1,66 +1,73 @@ # 第二次课后作业 - +
## 第5、6讲 支持向量机 -1. **简要说明支持向量机技术背后的基本思想，并说明软间隔的具体含义。** +
+ +1. 简要说明支持向量机技术背后的基本思想，并说明软间隔的具体含义。 + +> 支持向量机的基本思想是拟合类别之间可能存在的、最宽的缓冲区，其目的是使决策边界之间的间隔最大化，从而分隔出两个类别的训练实例。SVM 执行软间隔分类时，实际上是在完美分类和拟合最宽的街道之间进行妥协（也就是允许少数实例最终还是落在街道上）。 + +
+ +2. 简要说明核函数在非线性支持向量机中的作用。 + +> 为了解决原始特征空间中的非线性可分问题，需要通过非线性特征变换，把原始特征映射到高维空间，使得在高维空间中近似线性可分。但是直接计算变换后的高维特征矢量的内积，计算量太大，因此通过核函数，可以巧妙地解决这个问题：核函数能通过低计算量求值操作，来近似代替高维矢量的内积。因此，通过核函数隐含的非线性特征变换，结合线性支持向量机算法，就能把原空间中非线性可分的数据进行很好的分类。 + +
+ +3. 试证：位于超平面$b+x^{\top}\omega=\beta$中的点$x_p$到超平面$b+x^{\top}\omega=0$的代数距离为$d=\frac{\beta}{||\omega||}$。 - 支持向量机的基本思想是拟合类别之间可能存在的、最宽的缓冲区，其目的是使决策边界之间的间隔最大化，从而分隔出两个类别的训练实例。SVM 执行软间隔分类时，实际上是在完美分类和拟合最宽的街道之间进行妥协（也就是允许少数实例最终还是落在街道上）。 +
- +记$x_p$到超平面$b+x^{\top}\omega=0$的投影点为$x'_p$，两个平行超平面的法向量为$\omega$。 -2. **简要说明核函数在非线性支持向量机中的作用。** +先从几何方面看，矢量$(x_p-x'_p)$平行于法向量$\omega$，因此有 - 为了解决原始特征空间中的非线性可分问题，需要通过非线性特征变换，把原始特征映射到高维空间，使得在高维空间中近似线性可分。但是直接计算变换后的高维特征矢量的内积，计算量太大，因此通过核函数，可以巧妙地解决这个问题：核函数能通过低计算量求值操作，来近似代替高维矢量的内积。因此，通过核函数隐含的非线性特征变换，结合线性支持向量机算法，就能把原空间中非线性可分的数据进行很好的分类。 +$(x_p-x'_p)^{\top}\omega=||x_p-x'_p||||\omega||$ - +而点$x_p$到超平面$b+x^{\top}\omega=0$的代数间隔$d$实际上就是$||x_p-x'_p||$，因此有 -3. **试证：位于超平面$b+x^{\top}\omega=\beta$中的点$x_p$到超平面$b+x^{\top}\omega=0$的代数距离为$d=\frac{\beta}{||\omega||}$。** +$(x_p-x'_p)^{\top}\omega=d||\omega|| \cdots\cdots (1)$ - 记$x_p$到超平面$b+x^{\top}\omega=0$的投影点为$x'_p$，两个平行超平面的法向量为$\omega$。 +再从代数方面看，由于$x_p$和$x'_p$分别满足$b+(x_p)^{\top}\omega=\beta$和$b+(x'_p)^{\top}\omega=0$，两式相减 - 先从几何方面看，矢量$(x_p-x'_p)$平行于法向量$\omega$，因此有 - $$ - (x_p-x'_p)^{\top}\omega=||x_p-x'_p||||\omega|| - $$ - 而点$x_p$到超平面$b+x^{\top}\omega=0$的代数间隔$d$实际上就是$||x_p-x'_p||$，因此有 - $$ - (x_p-x'_p)^{\top}\omega=d||\omega|| \cdots\cdots (1) - $$ - 再从代数方面看，由于$x_p$和$x'_p$分别满足$b+(x_p)^{\top}\omega=\beta$和$b+(x'_p)^{\top}\omega=0$，两式相减： - $$ - (x_p-x'_p)^{\top}\omega=\beta \cdots\cdots (2) - $$ - 比较式（1）与式（2），有 - $$ - d=\frac{\beta}{||\omega||} - $$ - 证毕。 +$(x_p-x'_p)^{\top}\omega=\beta \cdots\cdots (2)$ +比较式（1）与式（2），有 +$d=\frac{\beta}{||\omega||}$ + +证毕。 +
+ +
## 第7、8讲 决策树与随机森林 -1. **如果训练集有100 万个实例，对叶节点样本数和数的深度均不加约束，则训练一个特征均为二值变量、平衡的二叉决策树，树的大致深度是多少？** +
- 一个包含$m$个叶节点的均衡二叉树的深度等于$\log_2{m}$的四合五入。通常来说，二元决策树训练到最后大体都是平衡的，如果不加以限制，最后平均每个叶节点一个实例。因此，如果训练集包含一百万个实例，那么决策树深度约等于$\log_2{10^6}$。因为$10^3\approx 2^{10}$，于是$10^6\approx 2^{20}$，$log_2{10^6}\approx log_2{2^{20}}=20$。实际上可能会更深一些，因为决策树通常不可能完美平衡。 +1. 如果训练集有100 万个实例，对叶节点样本数和数的深度均不加约束，则训练一个特征均为二值变量、平衡的二叉决策树，树的大致深度是多少？ - +> 一个包含$m$个叶节点的均衡二叉树的深度等于$\log_2{m}$的四合五入。通常来说，二元决策树训练到最后大体都是平衡的，如果不加以限制，最后平均每个叶节点一个实例。因此，如果训练集包含一百万个实例，那么决策树深度约等于$\log_2{10^6}$。因为$10^3\approx 2^{10}$，于是$10^6\approx 2^{20}$，$log_2{10^6}\approx log_2{2^{20}}=20$。实际上可能会更深一些，因为决策树通常不可能完美平衡。 -2. **CART算法按照基尼不纯度（基尼指数）进行结点划分，通常来说，子节点的基尼不纯度是高于还是低于其父节点？有没有可能，某个子结点的基尼不纯度高于其父结点的？给出算例说明你的结论。** +
- 一个节点的基尼不纯度通常比其父节点低，但是也存在一些特殊的情况，某个子结点的基尼不纯度大于其父结点。比如，二分类问题中，某个父结点有5个样本，在类别上分布为：1,2,1,1,1，基尼数为1-(1/5)2-(4/5)2=0.32。按照基尼不纯度分为两个子结点，左节点样本子集的类标记为1,2，右结点样本子集的类标记为1,1,1。显然左结点的基尼数为0.5，大约父结点。但是两个子结点的基尼数的加权和（0.2），仍然低于父结点，因此是一个合理的划分。 +2. CART算法按照基尼不纯度（基尼指数）进行结点划分，通常来说，子节点的基尼不纯度是高于还是低于其父节点？有没有可能，某个子结点的基尼不纯度高于其父结点的？给出算例说明你的结论。 - +> 一个节点的基尼不纯度通常比其父节点低，但是也存在一些特殊的情况，某个子结点的基尼不纯度大于其父结点。比如，二分类问题中，某个父结点有5个样本，在类别上分布为：1,2,1,1,1，基尼数为1-(1/5)2-(4/5)2=0.32。按照基尼不纯度分为两个子结点，左节点样本子集的类标记为1,2，右结点样本子集的类标记为1,1,1。显然左结点的基尼数为0.5，大约父结点。但是两个子结点的基尼数的加权和（0.2），仍然低于父结点，因此是一个合理的划分。 -3. **如果你已经在完全相同的训练集上训练了五个不同的学习器，并且它们都达到了95%的准确率，是否还有机会通过结合这些学习器来获得更好的结果？如果可以，该怎么做？如果不行，为什么？** +
- 如果你已经训练了五个不同的学习器，并且都达到了95% 的精度，你可以尝试将它们组合成一个投票集成，这通常会带来更好的结果。如果学习器模型之间非常不同（例如，一个SVM 分类器， 一个决策树分类器，以及一个Logistic 回归分类器等），则效果更优。如果它们是在不同的训练样本集（这是bagging 集成的关键点）上完成训练，那就更好了；如果不是，只要学习器模型非常不同，这个集成仍然有效。 +3. 如果你已经在完全相同的训练集上训练了五个不同的学习器，并且它们都达到了95%的准确率，是否还有机会通过结合这些学习器来获得更好的结果？如果可以，该怎么做？如果不行，为什么？ - +> 如果你已经训练了五个不同的学习器，并且都达到了95% 的精度，你可以尝试将它们组合成一个投票集成，这通常会带来更好的结果。如果学习器模型之间非常不同（例如，一个SVM 分类器， 一个决策树分类器，以及一个Logistic 回归分类器等），则效果更优。如果它们是在不同的训练样本集（这是bagging 集成的关键点）上完成训练，那就更好了；如果不是，只要学习器模型非常不同，这个集成仍然有效。 -4. **考虑如下二分类问题的数据集。** +
+ +4. 考虑如下二分类问题的数据集。 | **样本序号** | **A** | **B** | **类别** | | ------------ | ----- | ----- | -------- | @@ -75,18 +82,15 @@ | 9 | T | T | - | | 10 | T | F | - | - **（1）分别计算按照属性A和属性B划分时的信息增益。使用信息增益准则的决策树分类算法应该使用哪个属性？** - - **（2）分别计算按照属性A和属性B划分时的基尼指数。使用基尼指数的决策树分类算法应该使用哪个属性？** - - 解答：（陈封能，第2版，第3章，习题5） - - （1） - - ![78-4-1](D:\助教\2021-春-模式识别\本科-《机器学习与模式识别》\Course_MLPR\课后作业\pics\78-4-1.png) + （1）分别计算按照属性A和属性B划分时的信息增益。使用信息增益准则的决策树分类算法应该使用哪个属性？ -![78-4-2](D:\助教\2021-春-模式识别\本科-《机器学习与模式识别》\Course_MLPR\课后作业\pics\78-4-2.png) + （2）分别计算按照属性A和属性B划分时的基尼指数。使用基尼指数的决策树分类算法应该使用哪个属性？ -​ （2） +> 解答：（陈封能，第2版，第3章，习题5） +
+ +
+ +
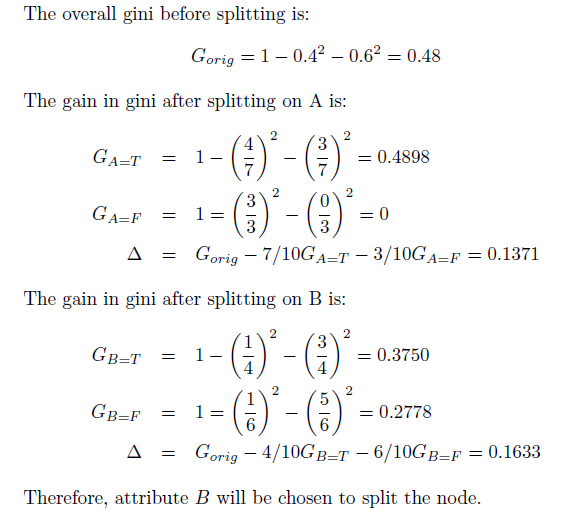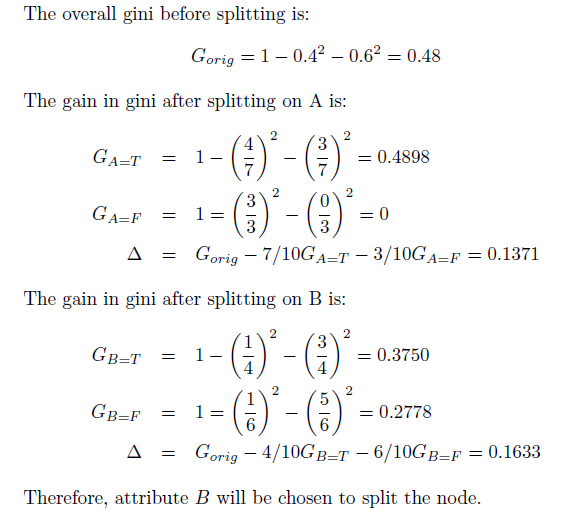+ -![78-4-3](D:\助教\2021-春-模式识别\本科-《机器学习与模式识别》\Course_MLPR\课后作业\pics\78-4-3.png) \ No newline at end of file